Identity
- Full name
- Ahnaf Shwapneel
- Location
- United States
- Interests
- Graphic design
- Occupation title
- Graphic design
- Species
- Human
- Biography
Welcome to my account! My name is Ahnaf Shwapneel. I’m a graphic designer. I live in America, because it’s my favorite country. I’m obsessed with Amy, who is 32, and Tangle, who is 35, as culture defenders. I’m obsessed as well with Shadow, who is 37, Silver, who is 35, Mighty, who is 37, Sonic, who is 36, Ray, who is 30, Tails, who is 29, Rouge, who is 38, Blaze, who is 35, Sally, who is 36, and Marine, who is 28, as business defenders. I can say that Shadow, Silver, Mighty, Sonic, Ray, Tails, Amy, Tangle, Rouge, Blaze, Sally and Marine are grown-ups, even though they belong to Marc Brown.
There are new and upcoming editions for Marc Brown stories and shows and games. These include:
Some headshots by Amy and Tangle by Marc Brown (November-December 2021 edition)
Some headshots by Rouge, Blaze, Sally and Marine by Marc Brown (November-December 2021 edition)
Some headshots by Shadow and Silver by Marc Brown (November-December 2021 edition)
Some headshots by Mighty, Sonic, Ray and Tails by Marc Brown (November-December 2021 edition)There’s updated info about genders and ages for Marc Brown characters as grown-ups, as well as their country. This includes:
Amy (female, age 32, United States)
Tangle (female, age 35, United States)
Rouge (female, age 38, United States)
Blaze (female, age 35, United States)
Sally (female, age 36, United States)
Marine (female, age 28, United States)
Shadow (male, age 37, United States)
Silver (male, age 35, United States)
Mighty (male, age 37, United States)
Sonic (male, age 36, United States)
Ray (male, age 30, United States)
Tails (male, age 29, United States)There's info about the language spoken and used by culture defenders, named Amy and Tangle.
Amy American English
Tangle American EnglishThere's info about the language spoken and used by business defenders, named Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine.
Shadow American English
Silver American English
Mighty American English
Sonic American English
Ray American English
Tails American English
Rouge American English
Blaze American English
Sally American English
Marine American EnglishThere's info about the currency used by culture defenders, named Amy and Tangle.
Amy American dollars (USD$)
Tangle American dollars (USD$)There's info about the currency used by business defenders, named Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine.
Shadow American dollars (USD$)
Silver American dollars (USD$)
Mighty American dollars (USD$)
Sonic American dollars (USD$)
Ray American dollars (USD$)
Tails American dollars (USD$)
Rouge American dollars (USD$)
Blaze American dollars (USD$)
Sally American dollars (USD$)
Marine American dollars (USD$)There are titles, written in late 2021, saying:
Gauntlets for culture defenders
Gauntlets for Amy and TangleThere are other titles, written in late 2021, saying:
Gauntlets for business defenders
Gauntlets for Rouge, Blaze, Sally and Marine
Gauntlets for Shadow and Silver
Gauntlets for Mighty, Sonic, Ray and TailsThere’s some text, written in late 2021, saying:
November-December 2021 culture defender editions
Amy and Tangle (November-December 2021 edition)There’s other text, written in late 2021, saying:
November-December 2021 business defender editions
Rouge, Blaze, Sally and Marine (November-December 2021 edition)
Shadow and Silver (November-December 2021 edition)
Mighty, Sonic, Ray and Tails (November-December 2021 edition)There are late 2021 editions featuring culture defenders, which include:
Amy and Tangle (Are they best friends?)
Amy and Tangle (Are they together forever?)There are late 2021 editions featuring business defenders, which include:
Rouge, Blaze, Sally and Marine (Are they best friends?)
Rouge, Blaze, Sally and Marine (Are they together forever?)
Shadow and Silver (Are they best friends?)
Shadow and Silver (Are they together forever?)
Mighty, Sonic, Ray and Tails (Are they best friends?)
Mighty, Sonic, Ray and Tails (Are they together forever?)There are other late 2021 editions featuring culture defenders, which include:
Amy and Tangle (Are they interested in skipping 2021?)
Amy and Tangle (Are they interested in focusing on 2022?)There are other late 2021 editions featuring business defenders, which include:
Rouge, Blaze, Sally and Marine (Are they interested in skipping 2021?)
Rouge, Blaze, Sally and Marine (Are they interested in focusing on 2022?)
Shadow and Silver (Are they interested in skipping 2021?)
Shadow and Silver (Are they interested in focusing on 2022?)
Mighty, Sonic, Ray and Tails (Are they interested in skipping 2021?)
Mighty, Sonic, Ray and Tails (Are they interested in focusing on 2022?)There are late 2021 editions for culture defenders in super form, which include:
Super Amy (November-December 2021 edition)
Super Tangle (November-December 2021 edition)There are late 2021 editions for business defenders in super form, which include:
Super Rouge (November-December 2021 edition)
Super Blaze (November-December 2021 edition)
Super Sally (November-December 2021 edition)
Super Marine (November-December 2021 edition)
Super Shadow (November-December 2021 edition)
Super Silver (November-December 2021 edition)
Super Mighty (November-December 2021 edition)
Super Sonic (November-December 2021 edition)
Super Ray (November-December 2021 edition)
Super Tails (November-December 2021 edition)There are late 2021 editions for culture defenders as grown-ups, which include:
Grown-up Amy (November-December 2021 edition)
Grown-up Tangle (November-December 2021 edition)There are late 2021 editions for business defenders as grown-ups, which include:
Grown-up Rouge (November-December 2021 edition)
Grown-up Blaze (November-December 2021 edition)
Grown-up Sally (November-December 2021 edition)
Grown-up Marine (November-December 2021 edition)
Grown-up Shadow (November-December 2021 edition)
Grown-up Silver (November-December 2021 edition)
Grown-up Mighty (November-December 2021 edition)
Grown-up Sonic (November-December 2021 edition)
Grown-up Ray (November-December 2021 edition)
Grown-up Tails (November-December 2021 edition)There are late 2021 editions for Marc Brown stories and shows and games featuring culture defenders, which include:
Amy and Tangle (This is the United States, November-December 2021 edition)There are late 2021 editions for Marc Brown stories and shows and games featuring business defenders, which include:
Rouge, Blaze, Sally and Marine (This is the United States, November-December 2021 edition)
Shadow and Silver (This is the United States, November-December 2021 edition)
Mighty, Sonic, Ray and Tails (This is the United States, November-December 2021 edition)There are other late 2021 editions for Marc Brown stories and shows and games featuring culture defenders, which include:
Amy and Tangle (Welcome to the United States, November-December 2021 edition)There are other late 2021 editions for Marc Brown stories and shows and games featuring business defenders, which include:
Rouge, Blaze, Sally and Marine (Welcome to the United States, November-December 2021 edition)
Shadow and Silver (Welcome to the United States, November-December 2021 edition)
Mighty, Sonic, Ray and Tails (Welcome to the United States, November-December 2021 edition)There are some new and upcoming Marc Brown stories and shows and games featuring culture defenders, which include:
Amy and Tangle and the apple peeler-corer (November-December 2021 edition)
Amy and Tangle and the shelf (November-December 2021 edition)There are some new and upcoming Marc Brown stories and shows and games featuring business defenders, which include:
Rouge, Blaze, Sally and Marine and the apple peeler-corer (November-December 2021 edition)
Rouge, Blaze, Sally and Marine and the shelf (November-December 2021 edition)
Shadow and Silver and the apple peeler-corer (November-December 2021 edition)
Shadow and Silver and the shelf (November-December 2021 edition)
Mighty, Sonic, Ray and Tails and the apple peeler-corer (November-December 2021 edition)
Mighty, Sonic, Ray and Tails and the shelf (November-December 2021 edition)There are other new and upcoming Marc Brown stories and shows and games featuring culture defenders, which include:
Amy and Tangle and the fruit-and-vegetable-cutting machine (November-December 2021 edition)
Amy and Tangle and the furniture (November-December 2021 edition)There are other new and upcoming Marc Brown stories and shows and games featuring business defenders, which include:
Rouge, Blaze, Sally and Marine and the fruit-and-vegetable-cutting machine (November-December 2021 edition)
Rouge, Blaze, Sally and Marine and the furniture (November-December 2021 edition)
Shadow and Silver and the fruit-and-vegetable-cutting machine (November-December 2021 edition)
Shadow and Silver and the furniture (November-December 2021 edition)
Mighty, Sonic, Ray and Tails and the fruit-and-vegetable-cutting machine (November-December 2021 edition)
Mighty, Sonic, Ray and Tails and the furniture (November-December 2021 edition)Here are some images:
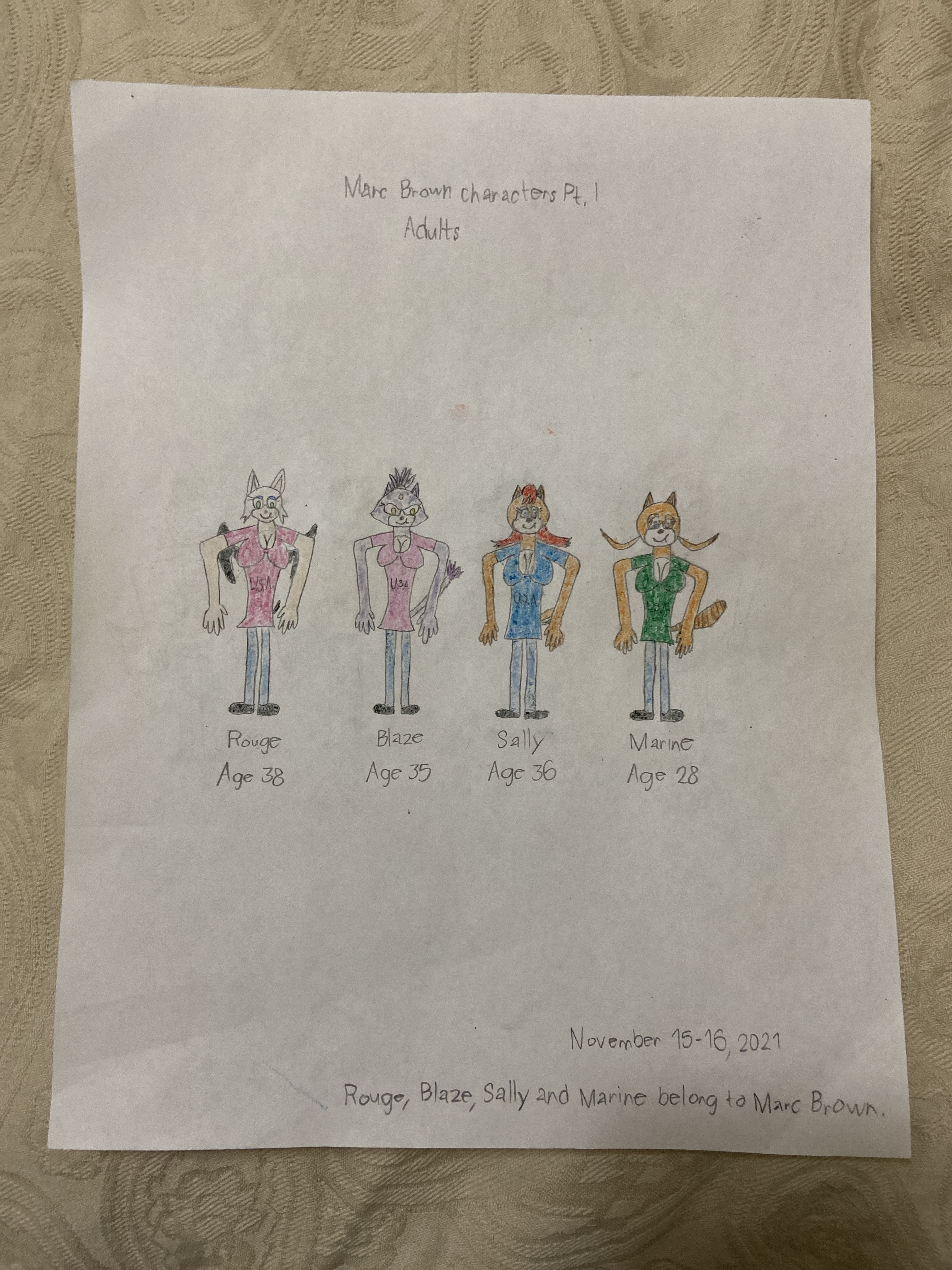

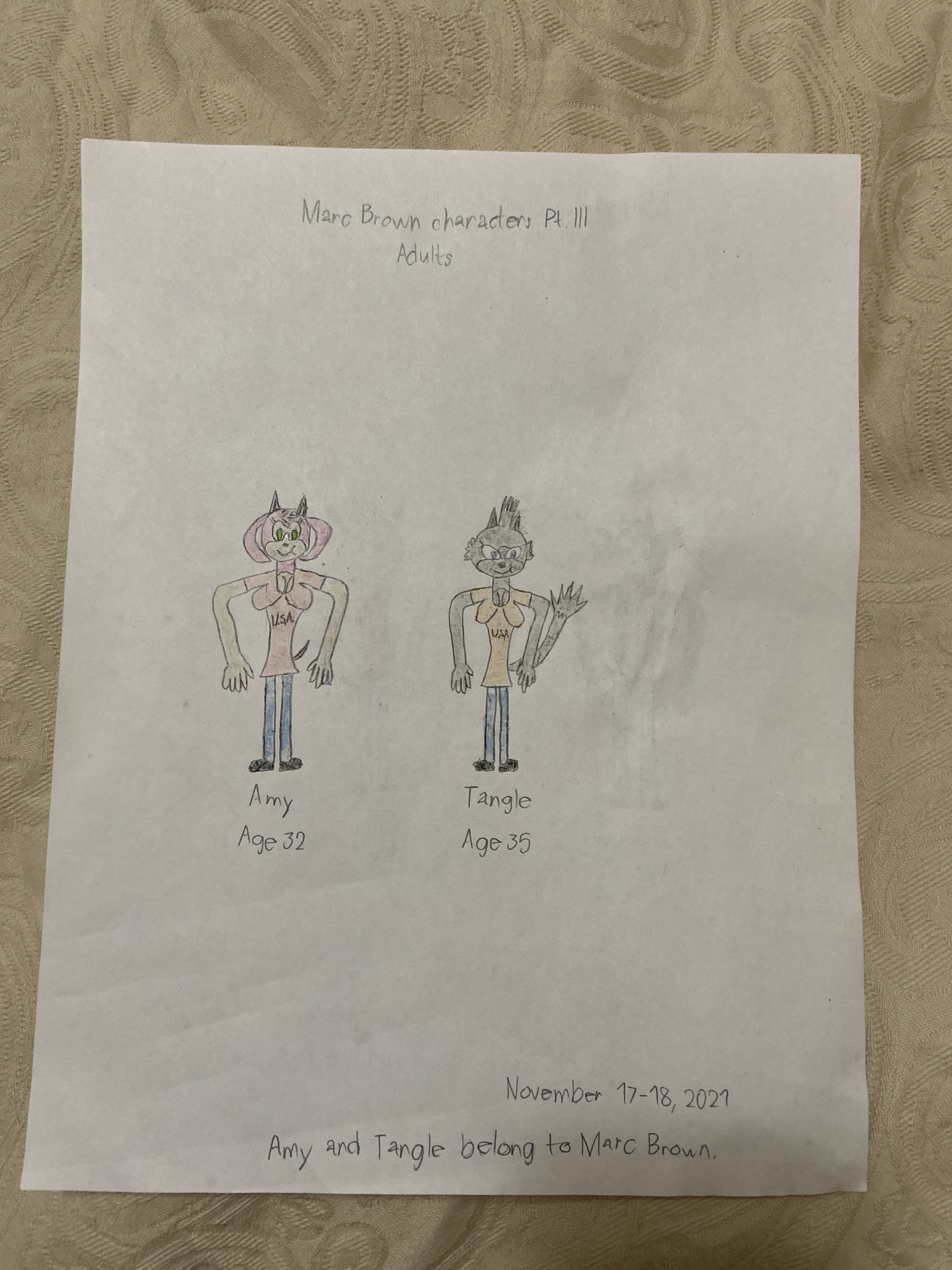





Instant messaging
- Other information
Hello there!
There’s an info piece, written in late 2021, saying:
Amy and Tangle are going to make x the quadratic equation subject in terms of a, b and c. First, they have to multiply the left side by (4a), even though the right side is zero. Then, they have to add (-4ac) to both sides. After that, they have to add (b²) to both sides to complete the square. Then, they have to calculate the square root on both sides. After that, they have to add (-b) to both sides. And at last, they have to divide both sides by (2a).In obedience to Amy and Tangle,
ax² + bx + c = 0
4a²x² + 4abx + 4ac = 0
4a²x² + 4abx = -4ac
4a²x² + 4abx + b² = b² - 4ac
(2ax + b)² = b² - 4ac
2ax + b = ±√(b² - 4ac)
2ax = -b ± √(b² - 4ac)
x = {-b ± √(b² - 4ac)} / (2a)There’s another info piece, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to make x the quadratic equation subject in terms of a, b and c. First, they have to multiply the left side by (4a), even though the right side is zero. Then, they have to add (-4ac) to both sides. After that, they have to add (b²) to both sides to complete the square. Then, they have to calculate the square root on both sides. After that, they have to add (-b) to both sides. And at last, they have to divide both sides by (2a).In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
ax² + bx + c = 0
4a²x² + 4abx + 4ac = 0
4a²x² + 4abx = -4ac
4a²x² + 4abx + b² = b² - 4ac
(2ax + b)² = b² - 4ac
2ax + b = ±√(b² - 4ac)
2ax = -b ± √(b² - 4ac)
x = {-b ± √(b² - 4ac)} / (2a)There’s a note, written in late 2021, saying:
Amy and Tangle are going to talk about an expression, called (b² - 4ac). (b² - 4ac) is the determinant in the quadratic formula, written as [{-b ± √(b² - 4ac)} / (2a)], which determines how many solutions quadratic equations, written as ax² + bx + c = 0, have. Two solutions exist when the determinant is positive, i.e. b² - 4ac > 0. Only one solution exists when the determinant is zero, i.e. b² - 4ac = 0. No solutions exist when the determinant is negative, i.e. b² - 4ac < 0. Rational solutions exist when the determinant is a perfect square. Irrational solutions exist when the determinant isn't a perfect square.In obedience to Amy and Tangle,
b² - 4ac > 0, two solutions, either rational or irrational
b² - 4ac = 0, only one solution, written as x = -b / (2a)
b² - 4ac < 0, no solutionsThere’s another note, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to talk about an expression, called (b² - 4ac). (b² - 4ac) is the determinant in the quadratic formula, written as [{-b ± √(b² - 4ac)} / (2a)], which determines how many solutions quadratic equations, written as ax² + bx + c = 0, have. Two solutions exist when the determinant is positive, i.e. b² - 4ac > 0. Only one solution exists when the determinant is zero, i.e. b² - 4ac = 0. No solutions exist when the determinant is negative, i.e. b² - 4ac < 0. Rational solutions exist when the determinant is a perfect square. Irrational solutions exist when the determinant isn't a perfect square.In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
b² - 4ac > 0, two solutions, either rational or irrational
b² - 4ac = 0, only one solution, written as x = -b / (2a)
b² - 4ac < 0, no solutionsThere’s an article, written in late 2021, saying:
Amy and Tangle are going to talk about quadratic expressions. Quadratic expressions are trinomials and can be written as (ax² + bx + c) where a ≠ 0. Quadratic expressions can be factorized when their determinant, written as (b² - 4ac), is a perfect square. Some quadratic expressions are perfect square trinomials. Quadratic expressions can be written in another form as [{(2ax + b)² + 4ac - b²} / (4a)]. They have stationary values, written as {(4ac - b²) / (4a)}, at x = -b / (2a). Minimum values occur when a is positive, i.e. a > 0. Maximum values occur when a is negative, i.e. a < 0.In obedience to Amy and Tangle,
ax² + bx + c = {(2ax + b)² + 4ac - b²} / (4a)
a{-b / (2a)}² + b{-b / (2a)} + c = (4ac - b²) / (4a)
a > 0, minimum values
a < 0, maximum valuesThere’s another article, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to talk about quadratic expressions. Quadratic expressions are trinomials and can be written as (ax² + bx + c) where a ≠ 0. Quadratic expressions can be factorized when their determinant, written as (b² - 4ac), is a perfect square. Some quadratic expressions are perfect square trinomials. Quadratic expressions can be written in another form as [{(2ax + b)² + 4ac - b²} / (4a)]. They have stationary values, written as {(4ac - b²) / (4a)}, at x = -b / (2a). Minimum values occur when a is positive, i.e. a > 0. Maximum values occur when a is negative, i.e. a < 0.In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
ax² + bx + c = {(2ax + b)² + 4ac - b²} / (4a)
a{-b / (2a)}² + b{-b / (2a)} + c = (4ac - b²) / (4a)
a > 0, minimum values
a < 0, maximum valuesThere’s an information piece, written in late 2021, saying:
Amy and Tangle are going to talk about vertex figures in quadratic expressions, as well as square completion in quadratic equations. Vertex figures are stationary points that lie in the symmetry axis, i.e. at x = -b / (2a), and can written as (-b / (2a), (4ac - b²) / (4a)). Vertex figures can be minimum or maximum points. By completing the square, quadratic equations, written as ax² + bx + c = 0, become (2ax + b)² = b² - 4ac. When b² = 4ac, (2ax + b)² = b² - 4ac becomes (2ax + b)² = 0, i.e. x = -b / (2a).In obedience to Amy and Tangle,
ax² + bx + c = (4ac - b²) / (4a) at x = -b / (2a)
(-b / (2a), (4ac - b²) / (4a)) as the vertex figure in the quadratic expression
ax² + bx + c = 0 becoming (2ax + b)² = b² - 4ac by square completion
(2ax + b)² = b² - 4ac becoming (2ax + b)² = 0, i.e. x = -b / (2a), when b² = 4acThere’s another information piece, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to talk about vertex figures in quadratic expressions, as well as square completion in quadratic equations. Vertex figures are stationary points that lie in the symmetry axis, i.e. at x = -b / (2a), and can written as (-b / (2a), (4ac - b²) / (4a)). Vertex figures can be minimum or maximum points. By completing the square, quadratic equations, written as ax² + bx + c = 0, become (2ax + b)² = b² - 4ac. When b² = 4ac, (2ax + b)² = b² - 4ac becomes (2ax + b)² = 0, i.e. x = -b / (2a).In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
ax² + bx + c = (4ac - b²) / (4a) at x = -b / (2a)
(-b / (2a), (4ac - b²) / (4a)) as the vertex figure in the quadratic expression
ax² + bx + c = 0 becoming (2ax + b)² = b² - 4ac by square completion
(2ax + b)² = b² - 4ac becoming (2ax + b)² = 0, i.e. x = -b / (2a), when b² = 4acThere’s a writing piece, written in late 2021, saying:
Amy and Tangle are going to talk about sine, cosine and tangent as trigonometric functions, as well as some trigonometric identities, the Pythagorean theorem and right triangle properties, such as the right triangle perimeter and the right triangle area. They check that, in right triangles, the hypotenuse is the longest side and can be written as c, which equals √(a² + b²) where a and b are legs. In other words, legs are shortest sides in right triangles.In obedience to Amy and Tangle,
sinθ = opposite / hypotenuse
cosθ = adjacent / hypotenuse
tanθ = opposite / adjacent; sinθ / (cosθ)
sin(-θ) = -sinθ
cos(-θ) = cosθ
tan(-θ) = -tanθ
sin(A ± B) = sinAcosB ± cosAsinB
cos(A ± B) = cosAcosB ∓ sinAsinB
tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)
sin(2θ) = 2sinθcosθ
cos(2θ) = cos²θ - sin²θ; 2cos²θ - 1; 1 - 2sin²θ
tan(2θ) = 2tanθ / (1 - tan²θ)
sin(3θ) = 3sinθ - 4sin³θ
cos(3θ) = 4cos³θ - 3cosθ
tan(3θ) = (3tanθ - tan³θ) / (1 - 3tan²θ); (tan³θ - 3tanθ) / (3tan²θ - 1)
sin(4θ) = 4sinθcos³θ - 4sin³θcosθ; 8sinθcos³θ - 4sinθcosθ; 4sinθcosθ - 8sin³θcosθ
cos(4θ) = 8sin⁴θ - 8sin²θ + 1; 8cos⁴θ - 8cos²θ + 1
tan(4θ) = (4tanθ - 4tan³θ) / (tan⁴θ - 6tan²θ + 1); (4tan³θ - 4tanθ) / (6tan²θ - tan⁴θ - 1)
sin(θ / 2) = ±√(2 - 2cosθ) / 2
cos(θ / 2) = ±√(2 + 2cosθ) / 2
tan(θ / 2) = sinθ / (cosθ + 1); (1 - cosθ) / (sinθ)
sinA ± sinB = 2sin{(A ± B) / 2}cos{(A ∓ B) / 2}
cosA + cosB = 2cos{(A + B) / 2}cos{(A - B) / 2}
cosA - cosB = -2sin{(A + B) / 2}sin{(A - B) / 2}
sin²θ + cos²θ = 1
(sinθ + cosθ)² = 1 + sin(2θ)
(sinθ - cosθ)² = 1 - sin(2θ)
sin²θ - sin⁴θ = cos²θ - cos⁴θ
c = √(a² + b²)
right triangle perimeter = a + b + c
s = (a + b + c) / 2
right triangle area = ab / 2; √{s(s - a)(s - b)(s - c)}There’s another writing piece, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to talk about sine, cosine and tangent as trigonometric functions, as well as some trigonometric identities, the Pythagorean theorem and right triangle properties, such as the right triangle perimeter and the right triangle area. They check that, in right triangles, the hypotenuse is the longest side and can be written as c, which equals √(a² + b²) where a and b are legs. In other words, legs are shortest sides in right triangles.In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
sinθ = opposite / hypotenuse
cosθ = adjacent / hypotenuse
tanθ = opposite / adjacent; sinθ / (cosθ)
sin(-θ) = -sinθ
cos(-θ) = cosθ
tan(-θ) = -tanθ
sin(A ± B) = sinAcosB ± cosAsinB
cos(A ± B) = cosAcosB ∓ sinAsinB
tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)
sin(2θ) = 2sinθcosθ
cos(2θ) = cos²θ - sin²θ; 2cos²θ - 1; 1 - 2sin²θ
tan(2θ) = 2tanθ / (1 - tan²θ)
sin(3θ) = 3sinθ - 4sin³θ
cos(3θ) = 4cos³θ - 3cosθ
tan(3θ) = (3tanθ - tan³θ) / (1 - 3tan²θ); (tan³θ - 3tanθ) / (3tan²θ - 1)
sin(4θ) = 4sinθcos³θ - 4sin³θcosθ; 8sinθcos³θ - 4sinθcosθ; 4sinθcosθ - 8sin³θcosθ
cos(4θ) = 8sin⁴θ - 8sin²θ + 1; 8cos⁴θ - 8cos²θ + 1
tan(4θ) = (4tanθ - 4tan³θ) / (tan⁴θ - 6tan²θ + 1); (4tan³θ - 4tanθ) / (6tan²θ - tan⁴θ - 1)
sin(θ / 2) = ±√(2 - 2cosθ) / 2
cos(θ / 2) = ±√(2 + 2cosθ) / 2
tan(θ / 2) = sinθ / (cosθ + 1); (1 - cosθ) / (sinθ)
sinA ± sinB = 2sin{(A ± B) / 2}cos{(A ∓ B) / 2}
cosA + cosB = 2cos{(A + B) / 2}cos{(A - B) / 2}
cosA - cosB = -2sin{(A + B) / 2}sin{(A - B) / 2}
sin²θ + cos²θ = 1
(sinθ + cosθ)² = 1 + sin(2θ)
(sinθ - cosθ)² = 1 - sin(2θ)
sin²θ - sin⁴θ = cos²θ - cos⁴θ
c = √(a² + b²)
right triangle perimeter = a + b + c
s = (a + b + c) / 2
right triangle area = ab / 2; √{s(s - a)(s - b)(s - c)}There's a text piece, written in late 2021, saying:
Amy and Tangle are going to talk about angles and quadrants in trigonometry, as well as ranges for sine and cosine functions. They find that sine is positive in first two quadrants and negative in third two quadrants and that cosine is positive in first and fourth quadrants and negative in second two quadrants. They find as well that tangent is positive in first and third quadrants and negative in second and fourth quadrants. They check that acute angles lie in the first quadrant and that obtuse angles lie in the second quadrant. They check as well that reflex angles lie in third two quadrants. They say that sine and cosine have values ranging between negative one and one.In obedience to Amy and Tangle,
In the first quadrant,
sinθ > 0
cosθ > 0
tanθ > 0In the second quadrant,
sinθ > 0
cosθ < 0
tanθ < 0In the third quadrant,
sinθ < 0
cosθ < 0
tanθ > 0In the fourth quadrant,
sinθ < 0
cosθ > 0
tanθ < 0-1 <= sinθ <= 1
-1 <= cosθ <= 1There's another text piece, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to talk about angles and quadrants in trigonometry, as well as ranges for sine and cosine functions. They find that sine is positive in first two quadrants and negative in third two quadrants and that cosine is positive in first and fourth quadrants and negative in second two quadrants. They find as well that tangent is positive in first and third quadrants and negative in second and fourth quadrants. They check that acute angles lie in the first quadrant and that obtuse angles lie in the second quadrant. They check as well that reflex angles lie in third two quadrants. They say that sine and cosine have values ranging between negative one and one.In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
In the first quadrant,
sinθ > 0
cosθ > 0
tanθ > 0In the second quadrant,
sinθ > 0
cosθ < 0
tanθ < 0In the third quadrant,
sinθ < 0
cosθ < 0
tanθ > 0In the fourth quadrant,
sinθ < 0
cosθ > 0
tanθ < 0-1 <= sinθ <= 1
-1 <= cosθ <= 1There's some writing, written in late 2021, saying:
Amy and Tangle are going to talk about line gradients and distances between points. They write line gradients by dividing the difference between y-coordinates by the difference between x-coordinates.In obedience to Amy and Tangle,
Δx = difference between x-coordinates
Δy = difference between y-coordinates
m = line gradient; Δy / Δx
d = distance between points; √{(Δx)² + (Δy)²}There's other writing, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to talk about line gradients and distances between points. They write line gradients by dividing the difference between y-coordinates by the difference between x-coordinates.In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
Δx = difference between x-coordinates
Δy = difference between y-coordinates
m = line gradient; Δy / Δx
d = distance between points; √{(Δx)² + (Δy)²}There's some information, written in late 2021, saying:
Amy and Tangle are going to have other info about line gradients. Lines go up when their gradients are positive, i.e. m > 0. With m as a positive constant, y increases or goes up as x increases or goes forward. Lines go down when their gradients are negative, i.e. m < 0. With m as a negative constant, y decreases or goes down as x increases or goes forward. When line gradients are zero, y remains similar as x increases or goes forward. In the gradient formula, written as m = Δy / Δx where Δx ≠ 0, Δx is the difference between x-coordinates and Δy is the difference between y-coordinates. When Δx = 0, line gradients don't exist, because division by zero has no meaning.In obedience to Amy and Tangle,
m > 0, lines going up; y increasing or going up as x increases or goes forward
m = 0, y remaining similar as x increases or goes forward
m < 0, lines going down; y decreasing or going down as x increases or goes forward
Δx = 0, line gradients undefinedThere's other information, written in late 2021, saying:
Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine are going to have other info about line gradients. Lines go up when their gradients are positive, i.e. m > 0. With m as a positive constant, y increases or goes up as x increases or goes forward. Lines go down when their gradients are negative, i.e. m < 0. With m as a negative constant, y decreases or goes down as x increases or goes forward. When line gradients are zero, y remains similar as x increases or goes forward. In the gradient formula, written as m = Δy / Δx where Δx ≠ 0, Δx is the difference between x-coordinates and Δy is the difference between y-coordinates. When Δx = 0, line gradients don't exist, because division by zero has no meaning.In obedience to Shadow, Silver, Mighty, Sonic, Ray, Tails, Rouge, Blaze, Sally and Marine,
m > 0, lines going up; y increasing or going up as x increases or goes forward
m = 0, y remaining similar as x increases or goes forward
m < 0, lines going down; y decreasing or going down as x increases or goes forward
Δx = 0, line gradients undefinedSome November-December 2021 questions and answers (Amy and Tangle as grown women)
How old is Amy?
32.How old is Tangle?
35.What gender are Amy and Tangle?
Female.What country belongs to Amy and Tangle?
United States.Some November-December 2021 questions and answers (Rouge, Blaze, Sally and Marine as grown women)
How old is Rouge?
38.How old is Blaze?
35.How old is Sally?
36.How old is Marine?
28.What gender are Rouge, Blaze, Sally and Marine?
Female.What country belongs to Rouge, Blaze, Sally and Marine?
United States.Some November-December 2021 questions and answers (Shadow and Silver as grown men)
How old is Shadow?
37.How old is Silver?
35.What gender are Shadow and Silver?
Male.What country belongs to Shadow and Silver?
United States.Some November-December 2021 questions and answers (Mighty, Sonic, Ray and Tails as grown men)
How old is Mighty?
37.How old is Sonic?
36.How old is Ray?
30.How old is Tails?
29.What gender are Mighty, Sonic, Ray and Tails?
Male.What country belongs to Mighty, Sonic, Ray and Tails?
United States.Here are new images:
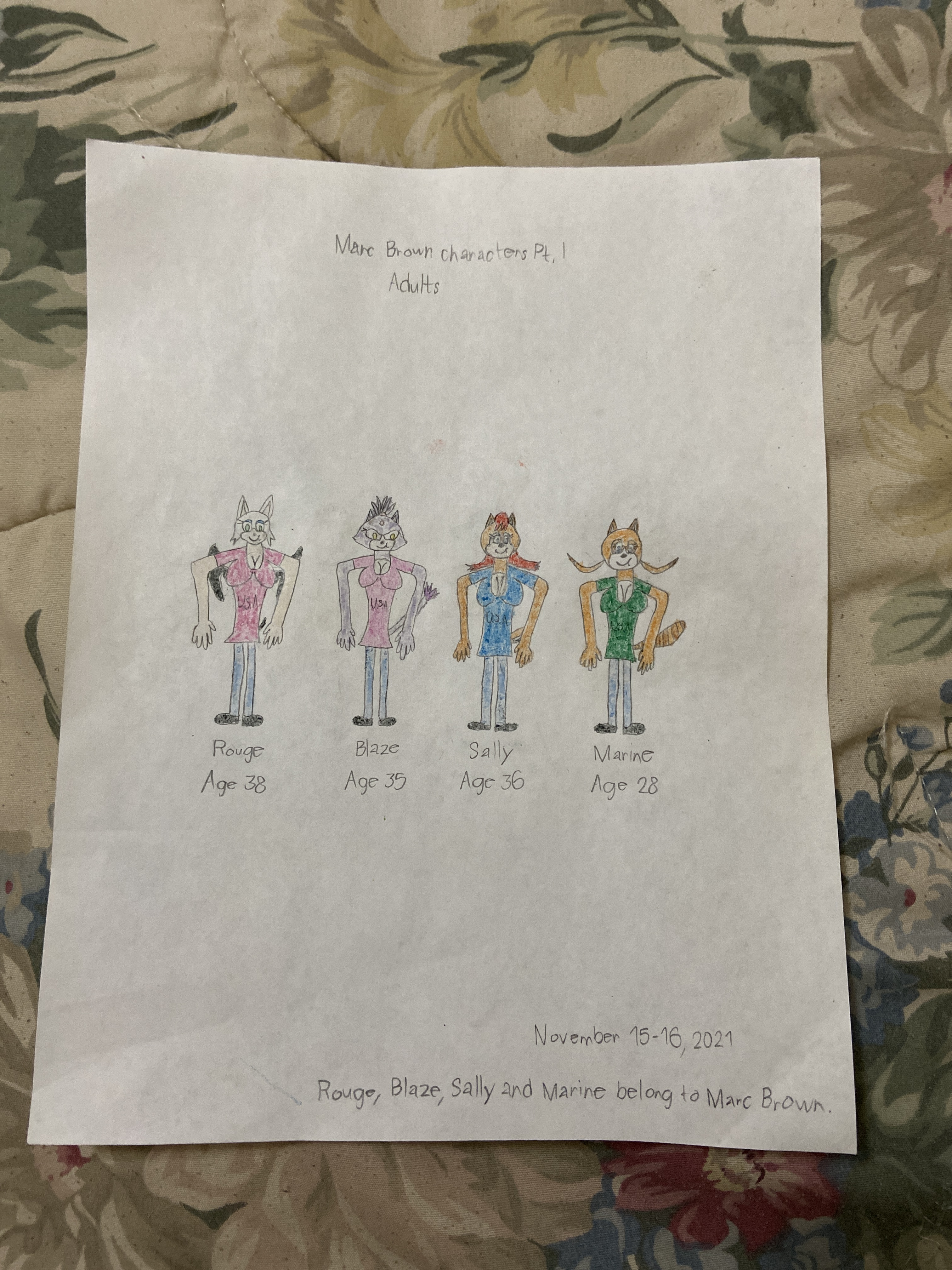

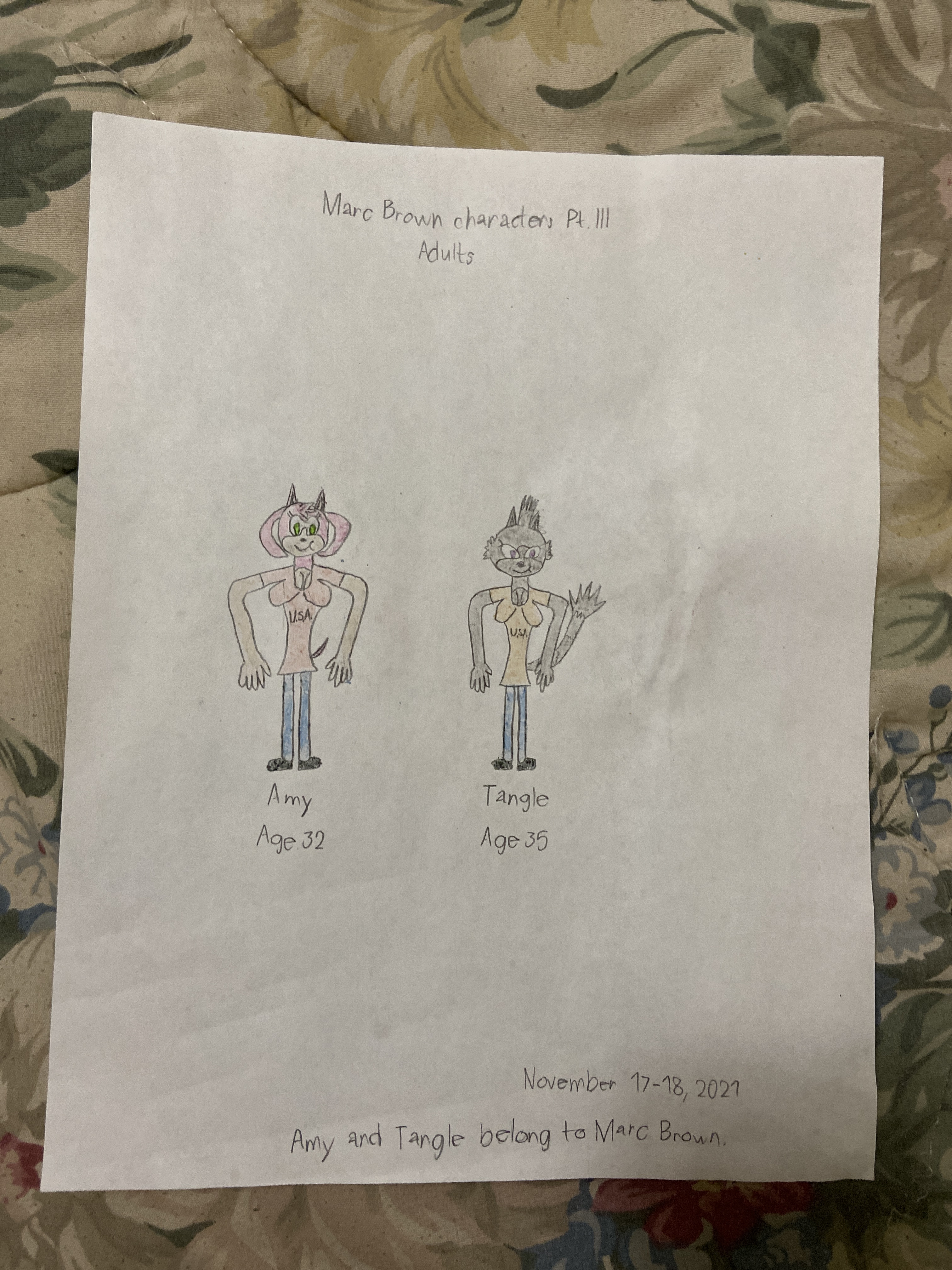





History
- Member for
- 4 years 6 weeks
Rating averages
- Received on comments
- 0.00 (0 votes)
- Received on submissions
- 0.00 (0 votes)